Lecture 4

2023-04-01

MIT OCW 14.01SC L4 - Preferences and Utility

MIT OCW 14.01SC - Lec 4 (Youtube)

  • So far: Overview of market, supply and demand curves.
  • Now: Taking a step back and understanding where supply and demand curves come from.
  • Starting with demand curve and consumer preferences. (First half of the course)
  • Consumer Behaviour - Utility Maximisation
    • Basically we assume all consumer behaviour comes from Utility Maximisation.
    • Consumer Preferences + Budget Constriant
    • What bundle of goods makes consumers best off?
    • Typically we will think about two goods (because two-dimensional graphs).
    • Three steps:
      • Assumptions about preferences. (Axioms.)
      • Translate the assumptions into mathematical function. (Utility function.)
      • Budget constraints.
  • Today's lecture: No budget constraints.
  • Unconstrained Preferences.
  • Three preference assumptions:
    1. Completeness: When comparing two bundles of goods, we prefer one or the other. Can't say "I'm not sure."
    2. Transitivity: If I prefer A > B and B > C then I prefer A > C.
    3. Non-satiation: (Most controversial?) More is always better. There may be diminishing returns but we will assume something > nothing.
  • Indifference Curves – Preference maps (graphical representation).
    • Example: Buy pizza or see movies?
    • Consider 3 choices:
      • 2 pizzas and 1 movie (A)
      • 1 pizza and 2 movies (B)
      • 2 pizzas and 2 movies (C)
    • Let's say we're indifferent between A & B, but we prefer C over A or B.
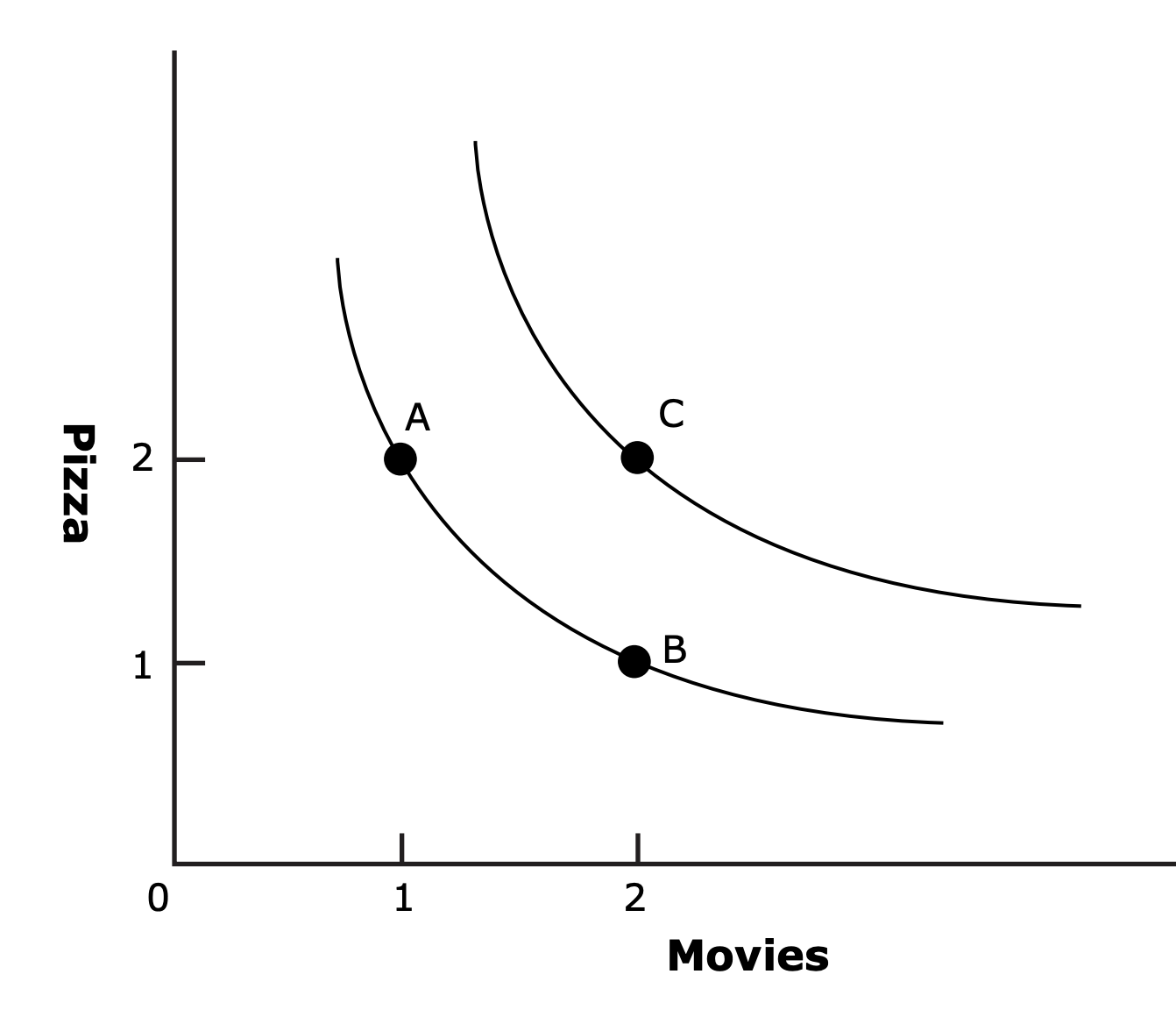
    • Indifference curves: indifference curve passing between A and B, C is on a different curve
      • A curve showing all possible combinations of consumption along which an individual is indifferent.
    • 4 Key properties of indiffernce curves.
      1. Consumers prefer higher indifference curves. (From non-satiation assumption.)
      2. Indifferent curves are always downward sloping. (From non-satiation assumption.)
      3. Indifference curves cannot cross.
      4. Completion implies => No more than one indifference curves through a point.
  • Next step: Utility.
    • Mathematical representation of preference.
    • Cannot tell absolute value of happiness, only useful for relative ranking.
    • Example: Assume for P pizzas and M movies, utility U = sqrt(P * M)
    • Marginal Utility (Key Concept!): How utility changes with each unit of input. (Derivative of utility function).
    • Assume diminishing marginal utility.
    • marginal utility = dU/dx_i, d^2 U / d(X_i)^2 < 0
  • Link between Utility and Preference maps?
    • Marginal rate of substitution.
      • Technically slope of indifference curve.
      • U(x, y) = 0 => ∂U/∂x dx + ∂U/∂y dy = 0 => dy/dx = -(∂U/∂x)/(∂U/∂y)
      • How many Y (pizzas) are you willing to trade off for one X (movie)
      • We always have diminishing marginal rate of substitution.
        • Increasing diminishing marginal rate of substitution would mean an indifference curve concave to the origin.
        • That wouldn't make sense. If you're willing to give up 1 Pizza for getting 1 movie, why would you give up 2 pizzas the next time to get 1 more movie? (* TODO: how to prove this formally?)