4. Experimentation Framework
2024-01-20
Running the model on GPU
Ok, we had left off with training the model on our small dataset of 100 games for 10 epochs. It was taking ~1 min on my machine to run it. However I noticed later that it was so slow because it was training on CPU!
To train it on the GPU, we only need a small change.
- chess_model = ChessModel()
+ # Transfer data to GPU if available
+ device = 'cuda' if torch.cuda.is_available() else 'cpu'
+
+ positions = positions.to(device)
+ valid_moves = valid_moves.to(device)
+
+ # Create the neural net
+ chess_model = ChessModel().to(device)
The .to(device) function transfers data to the GPU in pytorch and the whole
computation works on the GPU after that.
(torch) krkartikay@KartikayLegion:~/code/chess-sl$ time python train.py
...
Epoch 10, Average Test Loss: 0.1468
real 0m6.975s
user 0m6.034s
sys 0m1.003s
Now it's only taking ~7sec to train the model. That's almost a 10x improvement!
However, an important point to be noted here is that this is working only because our dataset is small enough to fit in the VRAM of the GPU in one go. If the dataset did not fit in the VRAM either of two things would happen:
- Either the CUDA drivers fail with an out of memory error! (best-case scenario), or,
- The training keeps running using our RAM ('shared memory') instead, but runs much more slowly and without any warnings.
In the second case we might think everything is running fine but actually there would be an issue, and everything might be much slower than it can be. Unfortunately (2) is the default behaviour of the CUDA drivers these days, but that can be changed in the settings (later...).
The proper solution would really be to stream the data to the GPU per-batch, or possibly even stream the data from disk to RAM (and from RAM to GPU) in a multithreaded dataloader, in case the dataset is big enough to not fit in RAM.
However let's implement that later and focus on experimenting with the network for now.
Optimising the network
We could now try out various things to optimise the network but keeping track of how various hyperparams are affecting the quality of the network is hard if we do it manually.
So we'll now develop a framework to keep track of the configs and run experiments by changing them systematically and noting the results.
Observations
The most important thing while doing experiments is to keep track of observations!
There's a risk of overengineering this part... For instance there are entire teams at google which handle metric collection and monitoring. But I'll try to keep things simple here.
Let's create an observer class which we can call observer.record(variable) on.
It will help us record and store the data.
# Observation framework
import os
import csv
import pickle
from matplotlib import pyplot as plt
class Observer:
def __init__(self, name, path="", suffix=""):
self.name = name
self.suffix = suffix
self.fullname = os.path.join(
path, name + (f"_{suffix}" if suffix else ""))
self.observations = []
def record(self, variable):
self.observations.append(variable)
def write_csv(self):
filename = (f"{self.fullname}.csv")
if len(self.observations) == 0:
return
with open(filename, "w") as file_handle:
csv_writer = csv.writer(file_handle)
csv_writer.writerows([x] for x in self.observations)
def save_pkl(self):
filename = (f"{self.fullname}.pkl")
pickle.dump(self.observations, open(filename, "wb"))
def plot(self):
filename = (f"{self.fullname}.png")
plt.figure()
plt.plot(self.observations)
plt.savefig(filename)
def avg(self):
return sum(self.observations) / len(self.observations)
To be honest it's nothing more than an array with some functions to save it, plot it, etc.
Let's see if we can plot the training and test loss with it now. (I've modified
the code a little bit to handle calling record on tuples/lists, and also
increased the epochs to 50.)
Relevant part of train.py now:
sgd_optimizer = SGD(chess_model.parameters(), lr=LEARNING_RATE)
loss_observer = Observer('loss', path="results/")
for epoch in range(NUM_EPOCHS):
for batch_num, (train_positions, train_valid_moves) in enumerate(train_dataloader):
sgd_optimizer.zero_grad()
move_probs = chess_model(train_positions)
loss = F.binary_cross_entropy(move_probs, train_valid_moves)
loss.backward()
sgd_optimizer.step()
if batch_num % 10 == 0:
print(f"{epoch+1}/{batch_num+1:3d}, Loss: {loss.item():.4f}")
# Test Evaluation
chess_model.eval()
total_test_loss = 0
with torch.no_grad():
for test_positions, test_valid_moves in test_dataloader:
test_move_probs = chess_model(test_positions)
test_loss = F.binary_cross_entropy(
test_move_probs, test_valid_moves)
total_test_loss += test_loss.item()
last_training_loss = loss.item()
average_test_loss = total_test_loss / len(test_dataloader)
loss_observer.record((last_training_loss, average_test_loss))
print(f"Epoch {epoch+1}, Average Test Loss: {average_test_loss:.4f}")
loss_observer.plot(['train_loss', 'test_loss'])
loss_observer.write_csv()
(Link to code so far at commit 09820da.)
Training Output:
(torch) krkartikay@KartikayLegion:~/code/chess-sl$ time python train.py
Loading data...
Loaded data. Shape:
positions : torch.Size([34879, 7, 8, 8])
moves : torch.Size([34879, 4096])
1/ 1, Loss: 0.6941
1/ 11, Loss: 0.6910
1/ 21, Loss: 0.6880
...
50/ 91, Loss: 0.1098
50/101, Loss: 0.1038
Epoch 50, Average Test Loss: 0.1048
real 0m23.212s
user 0m21.790s
sys 0m1.442
results/loss.png and results/loss.csv were created successfully.
loss.csv:
train_loss,test_loss
0.6621306538581848,0.6606337598391941
0.6188064217567444,0.6185613402298519
0.557918906211853,0.5588848718575069
...
loss.png: 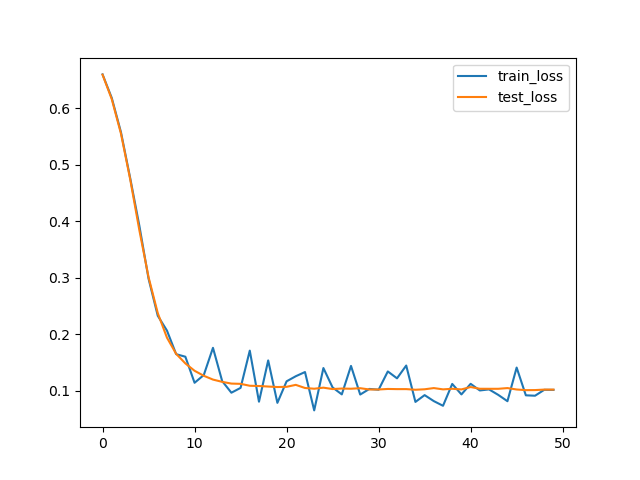
Experimentation framework
We need to optimise the neural net further! I think the loss of ~0.1 we're getting now is still too high. We could bring it down further by tweaking hyperparams and perhaps model architecture but let's develop a proper framework first to run experiments.
I want to be able to do something like this:
----------------------------------------------------------------------
config.py:
BATCH_SIZE = Config(default=128, values=[64, 128, 256, 512])
NUM_EPOCHS = Config(default=100, dev=10)
LEARNING_RATE = Config(default=0.1, values=[0.01, 0.03, 0.1, 0.3, 1, 3, 10])
----------------------------------------------------------------------
main.py:
def run_training():
train_model()
run_experiment(variables=[BATCH_SIZE, LEARNING_RATE],
function=run_training,
time_limit="5 mins")
----------------------------------------------------------------------
train.py:
from config import NUM_EPOCHS, LEARNING_RATE, BATCH_SIZE
def train_model():
...
optim = SGD(model.parameters(), learning_rate=LEARNING_RATE.get())
for epoch in range(NUM_EPOCHS.get()):
...
----------------------------------------------------------------------
That is, I specify all possible values of my hyperparameters and
run_experiment basically tries out all the possible combinations of the
variables I specify and stores all the results. So that I could see what the
effect of each variable is on the training, and also find out the optimal values
of hyperparameters which are giving me the best loss. I also want it to have a
dev mode where it runs experiments on a smaller scale which I can use to test
my code before doing a full training run.
Okay... implemented this... here's some of the relevant parts of the code:
class Experiment:
def __init__(self, variables=[], dev_mode=False):
self.variables: List[Config] = variables
self.dev_mode: bool = dev_mode
...
self.run_number: int = 0
self.selected_values: Dict[Config, Any] = {}
self.all_configs_results: Dict[str, Any] = {}
for config in ALL_CONFIGS:
config.expt = self
def get_config(self, config):
if config in self.selected_values:
return self.selected_values[config]
elif self.dev_mode:
return config.dev
else:
return config.default
def run_experiment(self,
function=None,
time_limit: int = 0):
value_combinations = itertools.product(
*[v.values for v in self.variables])
for values in value_combinations:
self.run_experiment_with_values(function, values)
def run_experiment_with_values(self, function, values):
self.selected_values = {
self.variables[i].name: values[i]
for i in range(len(self.variables))}
# run_experiment will run this function with selected values of
# variables
self.run_number += 1
print()
print("===================================================")
print(f"Experiment run {self.run_number}")
print("---------------------------------------------------")
print(f"Config for this run:\n{self.selected_values}")
print("===================================================")
start_time = time.time()
results = function()
end_time = time.time()
time_taken = end_time - start_time
print("===================================================")
print(f"Run finished in {time_taken:3.2f}sec.")
print("===================================================")
print()
self.all_configs_results.append({'run_num': self.run_number})
for key, value in self.selected_values.items():
self.all_configs_results[-1][key] = value
for key, value in results.items():
self.all_configs_results[-1][key] = value
self.all_configs_results[-1]['running_time'] = time_taken
for obs in ALL_OBSERVERS:
obs.set_path(path=self.results_path,
suffix=f"{self.run_number:03d}")
obs.plot()
obs.write_csv()
self.save_results()
Link to the full code at commit 1547c2a.
It's not really the best code I've written... I'm sure the design isn't as good as it could have been... but at least it works.
Here's what the results look like:
Analysing the results
Loading up the results.csv in excel and applying conditional formatting for
easier visualisation, here's what I get:
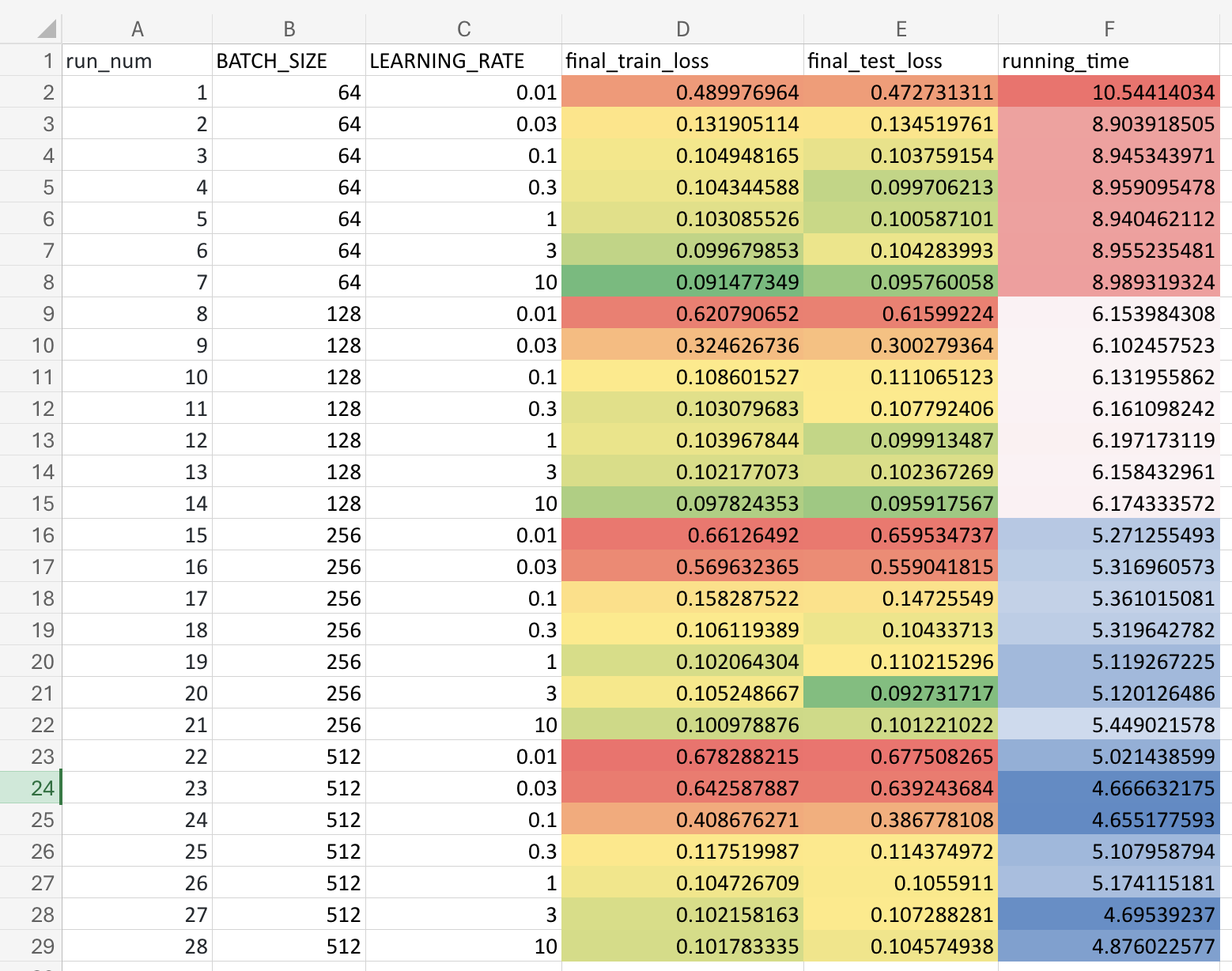
What're the main conclusions we can draw from this data? The main things I can notice are:
- Lower batch sizes take longer to compute (obvious)
- Smaller batch sizes train faster (lower loss even with low LR)
- Larger batch sizes requiring higher LR to converge (gradient competition?)
- Theoretically I would've guessed lower batch sizes to overfit more easily, and it kinda looks like it's going in that direction in run #6 & #7, train loss becoming slightly lower than test loss... (although I need to run it for more epochs to confirm this...)
- Conversely larger batch sizes should've generalised a bit more (run #20?)
- Final loss is around ~0.1-0.09 in all cases.
That's it for now. Next time we can try:
- Improve neural net architecture: adding conv layers etc.
- Evaluate the model by making it play games?
- More training data
- Visualisations...